BasicRL(3)-基于值的算法:Q-learning与DQN与改进

Q-learning

前面的Sarsa和TD算法之中, 我们的核心近似是 $q_{t}(s,a) \approx r_{t+1} + \gamma q_{t}(s_{t+1}, a_{t+1})$

我们再度展开整个 $Q(s,a)$ ，但并不是在Bellman方程之中，而是在Bellman最优方程之中 $Q^{*}(s,a) = E[R_{t+1} + \gamma max_a Q(S_{t+1},a)|S_t=s,A_t=a]$

Q: 为什么要在Bellman最优方程之中展开 $Q(s,a)$ 呢？

A: 核心原因是想要把算法改造成off-policy的, 来配合后面的经验回放等技术, 提高采样效率

前面的SARSA算法是on-policy的, 也就是说, 采样的轨迹必须是由当前策略产生的, 这样才能保证 $Q(s,a)$ 的收敛性，所以Sarsa里面使用了 $\epsilon$ -greedy策略, 以保证探索性; 但即使是这样, 其依然在采样效率上问题不小

$\epsilon$ -greedy策略, 调整超参数 $\epsilon$ 是一个复杂的工作, 且必然带来浪费
无论是MC还是TD, 在大方差数据的情况下效果都有缺陷, 使得 $\epsilon$ -greedy随时间探索性变低时, 可能还在采样到的局部最优里面，后续更无法跳出
在前期探索的数据, 想要将其保留下来, 后期继续使用(即采样比较贵，一个数据多用来更新几次策略), 但Sarsa无法做到

而我们在使用Bellman最优方程时, 实际上是在拟合函数 $f(s)=max_aQ(s,a)$ , 注意这里与动作a解耦了！

因而这个拟合的函数是policy无关的(policy只影响a的分布, 但我们拟合的函数不再是期望而是最大值)

从而这个函数的拟合就可以变成off-policy的, 我们可以用任意策略去采样数据, 再把采样得到的数据丢到算法里面迭代更新这个 $f(s)=max_aQ(s,a)$

这就是所谓的Q-learning算法, 也是我们的DQN算法的基础

def q_learning(explore_policy):
    Q = np.zeros((n_states, n_actions))
    for i in range(n_episodes):
        s = env.reset()
        while True:
            a = explore_policy(Q[s]) # 这里采用的探索策略可以是任意的，例如随机游走
            s_, r, done, _ = env.step(a)
            Q[s][a] = Q[s][a] + alpha * (r + gamma * np.max(Q[s_]) - Q[s][a])
            s = s_
            if done:
                break
    return Q

Deep Q-learning Network

从Q-learning进一步迭代到DQN的核心是把上面提到的 $f(s)=max_aQ(s,a)$ 的迭代更新用神经网络+梯度下降来做

也就是说, 我们把Q-learning的q[s][a]换成了了一个神经网络 $NN: S \times A \to scalar$

Q: 为什么要这样做?

A: 当动作空间是离散或者不太大的时候，保留a, 即前面的“表格方法” q[s][a]是可以的。但如果a是连续的呢？针对这样的连续问题, 一种方法当然是离散化, 但这只是权宜之计; 更好的方法肯定是使用一个函数来近似 $Q(s,a) = f(s,a)$ , 这样就能把a完全参数化，对任意a我们都可以给出一个不错的值了

当然，由上面的讨论我们也可以发现, 这个神经网络实际上只做一个类似插值的工作，所以一般而言其结构是很简单的, 就是几层MLP, 例如

class DQNNet(nn.Module):
    def __init__(self, n_states, n_actions, n_hidden=128):
    	super(DQNNet, self).__init__()
        self.fc1 = nn.Linear(n_states + n_actions, n_hidden) 
        self.fc2 = nn.Linear(n_hidden, n_hidden)
        self.fc3 = nn.Linear(n_hidden, n_actions) # Q(st, ai) for all ai in A
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

我们再举一个例子, 超级马里奥游戏

游戏的状态可以认为是当前屏幕画面(当然实际上会取几帧画面), 动作是上下左右跳等等

可以先用一个CNN来提取特征, 然后再用一个MLP来近似 $Q(s,a)$

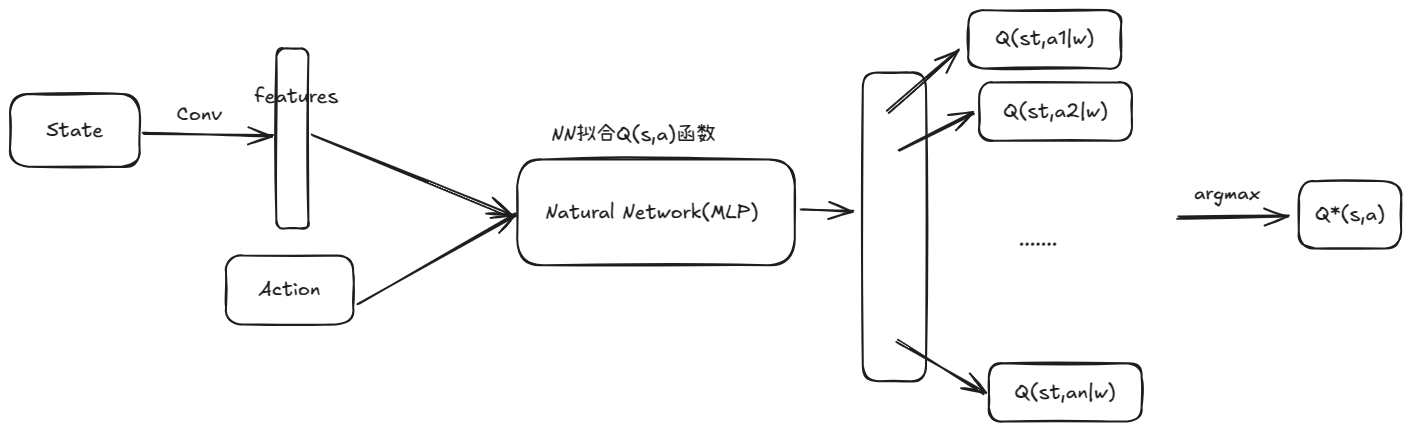
注意这个NN输出的是 $Q(s,a)$ 的向量, max是后续做的, 没有放在网络里面妨碍反向传播

这也是所谓"价值学习"的核心思想, 通过神经网络来近似 $Q(s,a)$ , 从而实现对任意状态动作对的价值估计

用DQN玩游戏的流程如下

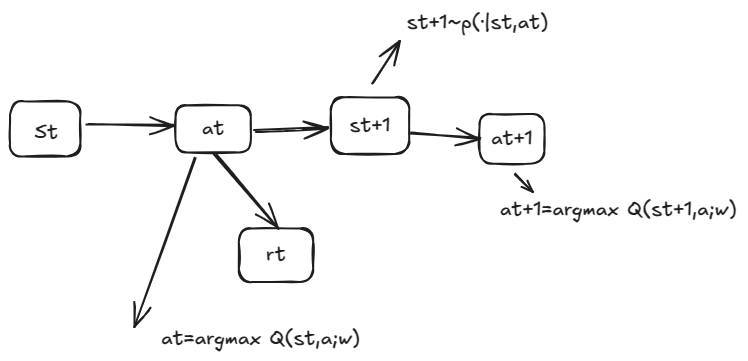
训练DQN的时候, 常用的是TD算法

如何设计网络的Loss呢？我们要让Q逼近实际的Q, 这就是我们之前TD算法做的事情, $L(w)=\frac{1}{2}(Q_t(s_t,a_t;w)-(r_t+\gamma max_aQ_t(s_{t+1},a;w))^2$ ，式子中的 $w$ 就是神经网络的权重，这个Loss就是TD error的平方

完整的DQN算法训练部分如下

def DQN(explore_policy):
    Q = DQNNet(n_states, n_actions)
    optimizer = torch.optim.Adam(Q.parameters(), lr=0.01)
    for i in range(n_episodes):
        s = env.reset()
        while True:
            a = explore_policy(q) # 这里采用的探索策略可以是任意的，例如随机游走
            q = Q(s,a)
            s_, r, done, _ = env.step(a)
            loss = F.mse_loss(q[a], r + gamma * torch.max(Q(s_,a)))
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            s = s_
            if done:
                break
    return Q

DQN的训练过程中, 关键的技术点是经验回放

经验回放: 之前提到的offline-policy的核心优势就在这里, 我们实际上可以进一步优化上面的训练过程, 将先前的 $(s_t,a_t,r_t,s_{t+1},a_{t+1})$ 的数据保存下来, 并在后续训练重用

具体来说, 我们可以采用一个大小为N的缓冲区, 每次训练的时候从中随机采样一部分数据，使用类似深度学习的mini-batch的想法, 这样可以有效地减小数据的相关性, 从而提高训练的效率

Q: 减小数据的相关性为什么能提高训练效率呢？

A: 论文这么说的, 算是一个实验结果, 也可以去看点理论分析

Q: N一般多大?

A: 一般而言, 在10万到100万量级都是可以的

一个示例的经验回放池

Transition = namedtuple('Transition',
                        ('state', 'action', 'next_state', 'reward'))


class ReplayMemory(object):

    def __init__(self, capacity):
        self.memory = deque([], maxlen=capacity)

    def push(self, *args):
        """Save a transition"""
        self.memory.append(Transition(*args))

    def sample(self, batch_size):
        return random.sample(self.memory, batch_size)

    def __len__(self):
        return len(self.memory)

其他优化的技术:

n-step: 之前我们提到的TD算法是一步的, 也就是说, 我们的更新是基于一个 $(s_t,a_t,r_t,s_{t+1},a_{t+1})$ 的数据, 但我们也可以考虑多步的TD算法, 例如n-step TD, 这样可以进一步提高训练的效率

优先经验回放：有些经验只是其他经验的重复, 也有些经验是比其他经验更重要的。如何衡量一条经验的重要度? 我们可以用TD error来衡量, err越大, 模型对其越“不熟”, 也就越重要

一般而言有两种优先级设定方法:

$p_t \propto |\delta_t| + \epsilon$ , $\epsilon$ 是一个小量防止为0
$p_t \propto \frac{1}{rank(t)}$ , 其中rank(t)是t在经验池中的排序

使用优先经验回放时，还需要注意对应步长的变化, 要维持先前收敛的稳定性质, 我们需要针对重要性调整学习率 $\alpha$ ，重要性大,采样多，步长小; 重要性小,采样少，步长大, 一般取 $\alpha = \alpha_0 (np_t)^{-\beta}, \beta \in (0,1)$ ， n是一个超参数，大致让中间重要的项的 $np_t$ 在1左右, 这样大的项指数减小，小的项指数增大

DQN高估问题与Double DQN, Dueling DQN

前面的DQN算法有一个问题, 就是对Q的高估

高估是怎么产生的? 来源于max, 也就是自举的那个操作: $Q(s,a) = r + \gamma max_aQ(s',a)$

我们知道max不是一个无偏的操作, 在 $Q(s,a)$ 为实际最优的时候, 上式成立, 而对于并不是最优的时候, 右式的迭代更新会使得 $Q(s,a)$ 比实际值大，想象 $Q = Q^{*} + \delta$ , $\delta$ 是一个随机变量的误差, $max Q$ 的分布就会比 $maxQ^{*}$ 的分布更偏大

如果max是均匀的，实际上也不是什么问题，因为我们实际上要的是策略, 是由 $\pi(s) = argmax_aQ(s,a)$ 决定的, 也就是决定策略的是不同动作的 $Q$ 相对值

但很可惜的是, max不是一个均匀放大的操作, 由于我们是采样更新的 $Q(s,a)$ ，被采样得更多 $(s,a)$ 对, 偏大得就会更多, 这最后会影响我们的策略

有两种解决方法:

target network

先讲target network, 我们引入一个新的网络（实际上是原始DQN网络的COPY） $Q(s,a;w^{-})$ ，它和 $Q(s,a;w)$ 的结构相同,但参数不同(更新频率不同)

在计算TD target和选择 $a^{*} = argmax_aQ(s_{t+1},a;w^{-})$ 的时候, 我们使用 $Q(s',a;w^{-})$ 来计算，其他时候用 $Q(s,a;w)$ 计算, 但更新 $w^{-}$ 的频率是比较低的, 例如每1000步更新一次(将 $Q(s,a;w)$ 重新赋值给 $Q(s,a;w^{-})$ )，从而减少自举带来的高估。也就是计算用 $w^{-}$ ，更新在 $w$ 上更新

double DQN

而对于double DQN, 它大体思想类似target network, 只基于一个观察改动了一个小地方

我们在选择 $a^{*} = argmax_aQ(s_{t+1},a;w)$ 的时候, 用 $argmax_aQ(s_{t+1},a;w)$ 来计算，这样可以减少高估

为什么？ $DoubleDQN = Q(s_{t+1},a^{*},w^{-}) \le max_aQ(s_{t+1},a, w^{-})=Target NN$ ，其中 $a^{*}$ 是 $w$ 下的最优动作

而后续的一个更好的改进是Dueling DQN

它引入了一个重要的东西叫优势函数 $A(s,a) = V(s) - Q(s,a)$

Dueling DQN并没有在公式上做太大的改进, 而是改进了网络结构

其捕获的关键点是, 我们得到的 $max_a Q(s,a)$ 收敛时, $V(s)$ 和 $A(s,a)$ 可能没有收敛, 而是一个偏大, 一个偏小

要让自举带来的高估问题减小甚至消失, 我们要让 $V(s) = E_a(Q(s,a))$ 也收敛

这样设计网络

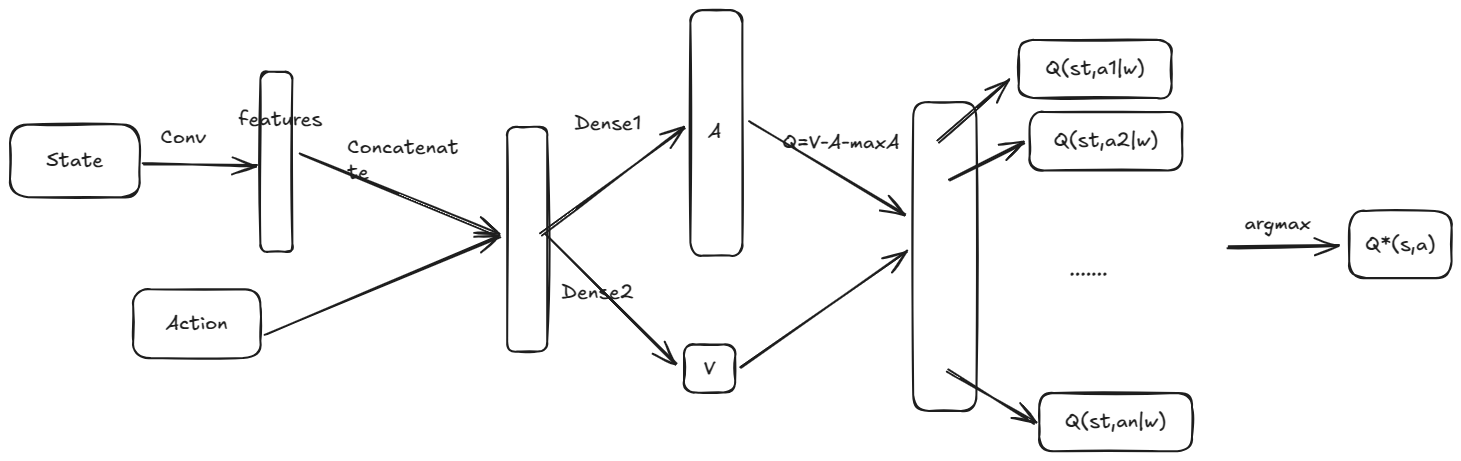
这里将中间的MLP表示Q分成了两个MLP, 一个输出n维表示A, 一个输入一个标量表示V, 最后再合并

关键就在于这个 $Q=V-A-max_aA$ 的操作, 这个依赖于当策略收敛(到始终选择最大Q的a)的时候, $max_aA$ =0, 而在其他时候, $max_aA$ 是一个负数, 从而减小了高估

实验表明的一个结论是把上式换成 $Q=V-A+mean_aA$ 效果更好, 但目前还不知道为什么

实验表明, Dueling DQN的减少高估的效果要优于Double DQN, Double DQN的效果要优于target network

但Dueling DQN也能同时和Double DQN结合, 也就是Double Dueling DQN, 这样效果更好

伪代码如下

from torchrl.data import ListStorage, PrioritizedReplayBuffer

class DuelingDQNNet(nn.Module):
    def __init__(self, n_states, n_actions, n_hidden=128):
    	super(DuelingDQNNet, self).__init__()
        self.fc1 = nn.Linear(n_states, n_hidden) 
        self.fc2 = nn.Linear(n_hidden, n_hidden)
        self.fc3 = nn.Linear(n_hidden, n_actions) # Q(st, ai) for all ai in A
        self.fc4 = nn.Linear(n_hidden, 1) # V(st)
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        A = self.fc3(x)
        V = self.fc4(x)
        Q = V + A - A.mean()
        return Q

def double_dueling_dqn_collect_experience(explore_policy)->PrioritizedReplayBuffer:
    # 初始化经验池
    experience_pool = PrioritizedReplayBuffer(alpha=0.7, beta=0.9, storage=ListStorage(10000))
    s = env.reset()
    a, r, s_, done = explore_policy(Q, s)
    while True:
        experience_pool.push((s, a, r, s_, done))
        if done:
            break
        s = s_
        a, r, s_, done = explore_policy(Q, s)

def double_dueling_dqn_train():
    Q = DuelingDQNNet(n_states, n_actions)
    Q_target = DuelingDQNNet(n_states, n_actions)
    optimizer = torch.optim.Adam(Q.parameters(), lr=0.01)
    experience_pool = double_dueling_dqn_collect_experience(explore_policy)
    T = 100 # 更新Q_target的频率
    for i in range(n_episodes):
        s = env.reset()
        batch = experience_pool.sample(batch_size)
        loss = 0
        for s, a, r, s_, done in batch
            q = Q(s,a)
            q_target = Q_target(s_,a)
            loss = F.mse_loss(q[a], r + gamma * q_target)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        if i % T == 0:
            Q_target.load_state_dict(Q.state_dict())
    return Q

BasicRL(3)-基于值的算法:Q-learning与DQN与改进

Q-learning​

Deep Q-learning Network​

DQN高估问题与Double DQN, Dueling DQN​

Q-learning

Deep Q-learning Network

DQN高估问题与Double DQN, Dueling DQN