12 posts tagged with "ai"

View All Tags

来本地部署大模型!

February 12, 2025 · 4 min read

ayanami

前言

这件事情的起因是这样的, 在开卷上机考想要部署一个本机大模型参考一下, 同时有同学和我讲qwen2.5-coder-7B非常的nice, 于是就有了下面这篇文章, 用ollama + docker部署的local LLM...

本地环境: Ubuntu24.04

以下是步骤

下载nvidia docker runtime

参考 https://docs.nvidia.com/datacenter/cloud-native/container-toolkit/latest/install-guide.html#installing-with-apt

apt

curl -fsSL https://nvidia.github.io/libnvidia-container/gpgkey | sudo gpg --dearmor -o /usr/share/keyrings/nvidia-container-toolkit-keyring.gpg \
  && curl -s -L https://nvidia.github.io/libnvidia-container/stable/deb/nvidia-container-toolkit.list | \
    sed 's#deb https://#deb [signed-by=/usr/share/keyrings/nvidia-container-toolkit-keyring.gpg] https://#g' | \
    sudo tee /etc/apt/sources.list.d/nvidia-container-toolkit.list

sudo apt-get update
sudo apt-get install -y nvidia-container-toolkit

设置 /etc/docker/daemon.json

{
    "default-runtime": "nvidia",
    "registry-mirrors": [
        "https://1nj0zren.mirror.aliyuncs.com",
        "https://docker.mirrors.ustc.edu.cn",
        "http://f1361db2.m.daocloud.io",
        "https://registry.docker-cn.com"
    ],
    "runtimes": {
        "nvidia": {
            "args": [],
            "path": "nvidia-container-runtime"
        }
    },
}

如果你需要代理, 参考配置加上

   "proxies": {
    "http-proxy": "http://127.0.0.1:7890",
    "https-proxy": "http://127.0.0.1:7890",
    "no-proxy": ""
  }

然后重启docker服务

sudo systemctl daemon-reload    
sudo systemctl restart docker

出现找不到"nvidia" runtime错误的, 检查有没有下载过docker desktop

下载过docker desktop的:

docker context ls
docker context use default

切换回default, 然后重启docker服务

下载ollama镜像

mkdir -p /data/containers/ollama/data
vi /data/containers/ollama/docker-compose.yml

docker-compose.yml

name: 'ollama'
services:
  ollama:
    restart: always
    image: ollama/ollama
    container_name: ollama
    runtime: nvidia
    environment:
      - TZ=Asia/Shanghai
      - NVIDIA_VISIBLE_DEVICES=all
    networks:
      - ai-tier
    ports:
      - "11434:11434"
    volumes:
      - ./data:/root/.ollama
networks:
  ai-tier:
    name: ai-tier
    driver: bridge
    ipam:
      config:
        - subnet: 172.22.1.0/24

启动

cd /data/containers/ollama
docker compose up -d

之后会拉ollama (2G)

验证成功

docker compose ps
# 得到结果应该如下
NAME      IMAGE           COMMAND               SERVICE   CREATED              STATUS              PORTS
ollama    ollama/ollama   "/bin/ollama serve"   ollama    About a minute ago   Up About a minute   0.0.0.0:11434->11434/tcp, :::11434->11434/tcp

下载模型

qwen2.5:7b建议换成其他的代码专用模型, 根据自己的电脑显卡配置决定参数量

空间占用 7b:5G, 3b: 2G, 1B:1G

docker exec -it ollama ollama pull qwen2.5:7b

成功结果这样

pulling manifest
pulling 00e1317cbf74... 100% ▕████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████  4.7 GB
pulling 4fa551d4f938... 100% ▕████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████   12 KB
pulling 8ab4849b038c... 100% ▕████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████   254 B
pulling 577073ffcc6c... 100% ▕████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████   110 B
pulling ad1518640c43... 100% ▕████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████   483 B 
verifying sha256 digest
writing manifest
removing any unused layers
success

验证

❯ docker exec -it ollama ollama list
NAME          ID              SIZE      MODIFIED    
qwen2.5:7b    845dbda0ea48    4.7 GB    2 hours ago    

What's next:
    Try Docker Debug for seamless, persistent debugging tools in any container or image → docker debug ollama
    Learn more at https://docs.docker.com/go/debug-cli/

开始服务

docker compose up -d

会在localhost:11434起一个服务, 浏览器输入后正常会有Ollama is running

前端套壳

ChatBox

直接去官网下载

https://chatboxai.app/zh/install

设置里面指定一下模型

aider版本

参考https://aider.chat/docs/config/dotenv.html设置一下OLLAMA_BASE_API的环境变量

之后aider --model ollama/qwen2.5:7b 即可

下载自己看官网(pip install aider-chat)

ok, 大功告成！

[可选] IDE插件

一个例子是Continue插件https://www.continue.dev/

参考官网, 据说vsc支持还行, jet bug不少

李沐dl笔记

January 20, 2025 · 30 min read

ayanami

vgg

内存占用大，推理慢（深），但效果好

卷积层参数小，全连接层最大问题是参数太大过拟合

所以最后一层全连接是很大的问题

大参数还有内存 bound 的问题

NiN

用卷积层替代全连接

两个 1*1 卷积无 padding, stride1 起全连接的作用(只做通道混合)

每个卷积后面跟两个全连接作为 NiN block

交替使用 NiN 块和 stride = 2 的 maxpooling 逐步减小高宽和增大通道数

最后使用全局平均池化得到输出(通道数 = 分类个数)

打印结构:

for layer in net:
    X = layer(X)
    print(layer.__class__.__name__, "output shape:\t", X.shape)

超级宽的 hidden layer: 非常容易过拟合

泛化性提高-> 收敛变慢

全连接的方案: 非常强, 收敛很快

GoogLeNet

inception 块: 不做选择, 全都要

output = output1 + o2 + o3 + o4

o1 = conv1x1

o2 = conv1x1 + conv3x3, padding 1

o3 = conv1x1 + conv3x3, padding 1 + conv5x5, padding 2

o4 = 3x3 maxpool, padding 1

四条路径从不同层面抽取信息, 在输出通道合并 concatenation

四条路径分配不同的通道数(你认为那种模式哪个通道的信息更重要)

降低通道数来控制模型复杂度

googlenet 5 段, 9 个 inception 块

不降低维数的 1x1 卷积就是通道融合

第一个 stage 总是把通道数拉上去, 高宽减下去, 先筛选出足够多的特征

v2: batch normalization

v3: 5x5-> 3x3, 5x5-> 1x7+7x1(单长和单宽)

v4: 残差连接

优点是模型参数少, 计算复杂度低

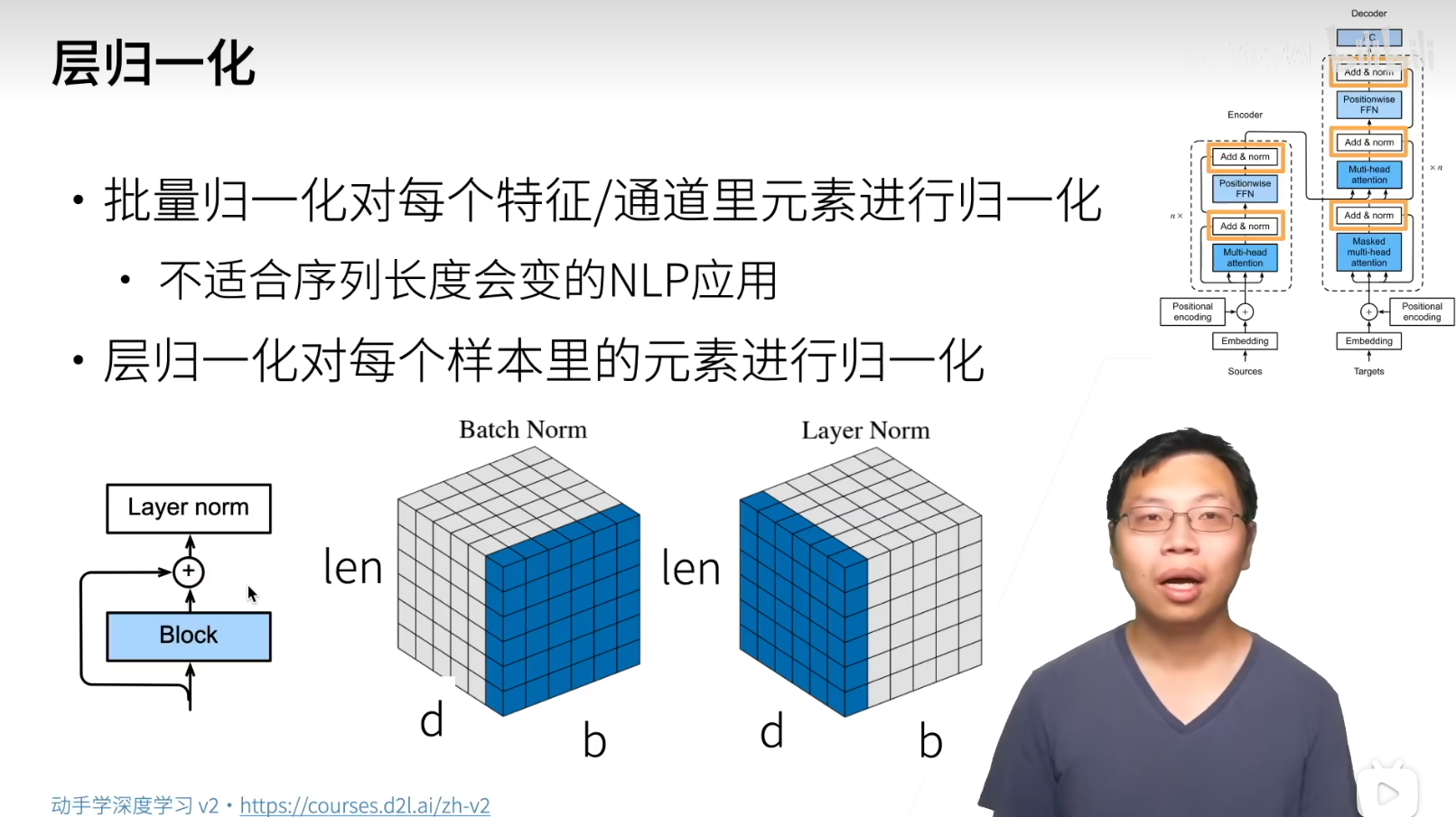
批量归一化

损失出现在最后, 后面的层训练快

反向传播: loss 在顶层, 数据在最底部, 底部的层(前面的层)训练慢, 底部层一变, 所有都得跟着变

导致离 loss 近的后面层需要重新学习多次, 导致收敛变慢

有没有方法让学习前面层的时候避免变化后面层?

批量归一化: 将分布固定, 来让输出模式稳定一些, 固定小批量的均值和方差

正则化, 将数据分布固定为 $N(0,1)$ 正态分布, 数据的修改只是在变化正态分布的超参数, 限制变化不要太剧烈

对于全连接, 作用 在激活函数前面, 作用在特征维度

对卷积, 作用在通道维

效果太好了, 原始论文觉得是减少内部协变量转移, 后续发现 可能就是等效于在每个小批量里面加入噪音来控制模型, 均值近似于随机偏移, 方差近似于随机缩放

因此没必要和丢弃混合使用

加速收敛(模式更稳定之后可以把 lr 调得更大), 但一般不改变模型精度

根据内存挑 batch size, 不能太大也不能太小, 然后调学习率和 epoch

ResNet

残差的重要性不必多言

深网络必有残差思想

新硬件

DSP 主要做数字计算处理长指令, FPGA 可编程阵列

工具链质量良莠不齐, 一次 "编译" 需要很久

AI ASIC: Google TPU eg

核心 systolic array, 专门做大矩阵乘法 2d 计算单元(PE)阵列, 卷积换成矩阵乘法

一般的矩阵乘: 切开和填充匹配 SA 大小

批量输入来降低延时, 其他硬件单元来处理别的 NN 操作子, 例如激活层

多卡并行

数据并行(切割小批量), 模型并行(切割模型, 适用于模型太大的时候),

all reduce: 将所有 gpu 的结果放到一个 gpu 上, 然后相加, 加完再复制回其他 gpu

nn.parallel.scatter

nn.DataParallel

多卡时也要相应的加大 batchsize 和 lr

大 batch size 在小模型上会采出重复样本导致浪费和一定程度上的过拟合

分布式

GPU 和 GPU 通信快, 和 CPU 通信慢, 和交换机网卡更慢

类似存储器山

解法是把 parameter server 尽量从 cpu 搬到 gpu 上

这样简单的 parameter 迁移分配就能在 gpu 本地完成, 不涉及到 cpu 的 copy(感觉像 DMA)

每个 worker 拿参数, 复制到 GPU 上, 每个 GPU 算自己的梯度, GPU 梯度求和, 传回服务器, 再更新, 回发

类似 mr, server mapper, 本地 gpu 完成计算和 combine, 在 server reduce

同步 SGD, 每个 worker 同步计算一个批量

所以需要调 batch size, 来针对并行省下的时间与通信开销做 trade off

实践:

大数据集
好的 GPU-GPU 和机器-机器带宽
高效的数据读取和预处理
好的计算(FLOP)和通信(model size)比 Inception > ResNet > AlexNet
足够大的 batch size
高效优化算法（因为 batch size 变大了, 如何适配）
更复杂的分布式有异步, 模型并行

一般 N 个类, batch size 差不多到 10N 再往上就不太能 fit 了

数据增广

已有数据集让他有更多多样性

在语言里面加背景噪音
改变图片的亮度, 颜色, 形状

一般的做法: 原始数据在线生成, 随机增强

测试不做增强

翻转:

左右翻转, 上下翻转
切割, 随即高宽比, 随机大小, 随机位置

其他:

高斯模糊
锐化
变形
滤镜
马赛克（相当于遮挡, 逼着去看全局）
...

从实际部署的场景反推需要什么样的增强

异常检测, 偏斜数据, 重采样, 增广

mixup 增广: 有效但不知道为什么

torchvision.transforms

微调(迁移学习)

标注一个数据集很贵

希望在大数据集上做好的东西, 能以小代价迁移到小数据集上

神经网络分层两块: 特征提取+线性分类

dl: 让特征提取变得可以学习, 而不是人来提取特征

训练:

更强正则化
更小学习率
更少的数据迭代

源数据集远复杂于目标, 微调效果更好

固定一些层, 固定底部一些层的参数, 不参与更新

低层次的特征更加通用

小 trick, 微调的时候最后一层用大学习率, 前面用小的

迁移的也不能差太大, 否则效果很可能不够好

目标检测

bounding box

锚框: 提出多个被称为锚框的区域, 预测每个框里面是否有关注的物体, 如果是, 预测锚框到真实框的偏移

交并比 IoU

每个锚框是一个训练样本, 要么标注成背景, 要么关联一个真实边缘框

可能生成大量锚框, 导致大量的负类样本

选择合适的锚框(赋予锚框标号):

先生成一堆框, 之后算锚框 i 和真实框 j 的 IoU, 在 i, j 之中找最大的, 就得到了一组锚框和真实框的对应

然后从集合中剔除这个锚框 i 和边缘框 j(删除矩阵行列), 再找下一组

重复直到真实框为空, 这就是正类样本, 剩下的锚框挑一些作为负类样本

锚框生成: 一种固定切分画格子

NMS 非极大抑制: 合并相似的预测框

选中非背景类的最大预测值
去掉所有和它 IoU 大于阈值的预测
重复直到所有预测要么被选中, 要么被去掉

生成锚框的另一种示例方法

宽度 $ws\sqrt r$ , 高度 $hs/\sqrt{r}$

对给定几组 $(s,r)$ 对每(n)个像素生成

算法的核心之一: 如何生成高质量锚框

锚框到偏移的算法: 多种多样

autogluon

工业界很少用模型融合和测试增强, 计算代价过高

通常固定模型超参数, 简单模型, 精力花在提升数据质量和加入的新数据

RCNN:

启发式搜索算法选择锚框

预训练模型对每个锚框抽取特征

训练一个 SVM 对类别分类

训练一个线性回归来预测偏移

RoI pooling

锚框均匀分割 mxn, 输出每块里面的最大值

不管锚框多大, 总是输出 mn

Fast RCNN

不再对每一个锚框抽取特征

而是将所有的锚框丢进 cnn(输入里面对应的映射区域), 一次 CNN 对整个图片抽取

Faster RCNN: 使用区域提议网络代替启发式搜索来获得更好的锚框

2-stage

Mask RCNN 如果有像素级别的编号, 给每个像素做预测, 用 FCN 利用信息

Faster RCNN: 速度非常慢, 精度高

SSD: single stage

基础网络抽特征, 多个 conv 减半高宽

每段都生成锚框

底部段拟合小物体, 顶部段拟合大物体

对每个锚框预测类别和边缘框

yolo: 追求快

ssd 锚框大量重叠, 浪费计算

均匀切分 SxS 个锚框, 每个锚框预测 B 个边缘框

后续有许多微调和改进

工业常用

非锚框: 例如 central net

语义分割

像素级分类

应用: 背景虚化, 路面分割

另一个相近的概念: 实例分割

数据集: 输入是图片, label 也是图片(每个像素的值就是 label)

crop: 怎么做, 对输入进行裁剪, 在 label 上也要相对应的裁剪

拉伸也是需要特殊处理的

旋转? 一种是可以加一个 label 是旋转角度, 另一个是可以在转完的斜框上涨再画一个大框框住斜框

人像: 难点在光照, 阴影和背景

人像语义分割: pretrain model 已经很成熟

转置卷积

卷积的问题：不能很有效的增加高宽

类似语义分割这种-> 卷积不断减小高宽, 会影响像素级别的输出

$Y[i:i+h, j:j+w] += X[i,j] \times K$

增大输入高宽

为什么是转置卷积:

卷积等价于矩阵乘法 $Y = VX$ , 转置卷积就是 $Y = V^{T}X$

nn.ConvTranspose2d

卷积是下采样, 卷积是上采样

转置卷积与线性插值: 可以用线性插值作为转置卷积核的初始值

FCN

全连接卷积神经网络

用 dl 做语义分割的最早工作

用转置卷积替换 CNN 最后的全连接层+全局池化

先过 1x1 conv 压缩通道
再过转置卷积拉大图片, 得到像素级别的切分
- 思想是每个像素的的 label 信息这个 feature 应该存在 channels 里面

net = nn.Sequential(*list(pretrained_cnn.children()))[:-2]

可以用双线性插值的矩阵初始化转置卷积层的 kernel

loss: 由于每一个像素都有了 label

所以在矩阵上做均值再 cross_entropy

样式迁移

基于 CNN 的样式迁移

核心思想: 训练一个 CNN, 将他作用在内容图片上得到输出, 在样式图片上得到输出

而输出图片在内容层上的输出和内容图片在内容层上的输出相近(content loss)

输出图片在样式层上的输出和样式图片在样式层上的输出相近(style loss)

训练的不是 CNN, 而是输入网络的的“输出图片”

哪些层是“style layer”, 哪些是 "content layer"?

样式: 最小, 中间和上层, 较均匀

样式有全局的特征和局部的特征, 各个尺度均有

内容: 偏末尾的层, 靠近 loss

允许内容上更多的变形

内容损失可以是简单的 MSE

元素值, 通道里面的值, 认为是内容

样式损失? 通道内部和之间的统计分布, 认为是样式

分布匹配, 一阶平均值, 二阶协方差, 用二阶就还不错

最后: tv_loss, 不要有噪点, 每个像素和周围像素不要差太多, 计算每个与周围的 MSE 再求平均

这几个损失如何加起来? 加权平均, 权值是超参数

style 一般更重要, 例如 content:style:tv=1:1000:10

这几个超参数的调整是训练几次之后, 观察三种 loss, 调到差不多大小得出的

不更新: y.detach()

卷积只作为抽特征

麻烦: 后续技术, GAN, 使用 CNN 接收随机输入生成图片等

序列模型

标号和样本是一个东西: 自回归模型 t-k ~ t-1 -> t

方法 A: 马尔可夫假设: 假设当前数据只和 k 个过去数据点相关

方法 B: 潜变量模型: 引入潜变量 $h_t$ 来表示过去信息 $x_t = p(x_t|h_t)$ , $h_t = f(x_1,...x_{t-1})$

那我们就可以将预测拆成两步:

$h_t = Model1(h_{t-1}, x_{t-1})$
$x_t = Model2(h_t, x_{t-1})$

文本预处理

预处理的核心是分词

GPU 上存算的是 token 索引而非字符串

语言模型:

给定文本序列, 估计联合概率

做预训练模型
生成文本
判断多个序列之中哪个更常见

简单方法: 基于计数建模

序列很长的时候, 由于文本量不够大, 可能 $n(x_1,...x_t)\le 1$

使用马尔可夫假设缓解, n 元语法假设, 假设只和前 n 个词相关

以二元为例, 则有 $p(x_1,x_2,x_3,x_4) = \frac{n(x_1)}{x1} \frac{n(x_1,x_2)}{n(x1)} \frac{n(x_2,x_3)}{n(x2)} \frac{n(x_3,x_4)}{n(x3)}$

RNN

更新隐藏状态: $h_t = \phi (W_{hh}h_{t-1} + W_{hx}x_{t-1} + b_h)$

输出: $o_t = \phi (W_{ho}h_t + b_o)$

训练的模型: $W_{hh}, W_{hx}, W_{ho}, b_h, b_o$

如果没有 $W_{hh}h_{t-1}$ 就是 MLP

loss 设计: 困惑度 perplexity

把输出看成是词典大小为 label 数量的话, 可以用交叉熵, 然后对整个句子取平均

但实际不是用这个, 而是用 exp(平均交叉熵)

梯度裁剪: 在 T 个时间步上的梯度, 反向传播 O(T)矩阵乘法, 梯度爆炸

如果梯度长度超过 $\theta$ , 变回 $\theta$

$g \times min(1, \frac{\theta}{||g||}) \to g$

更多的 RNN:

1 对多: 文本生成
多对 1: 文本分类
多对多: 问答, 机器翻译
多对多: tag 生成

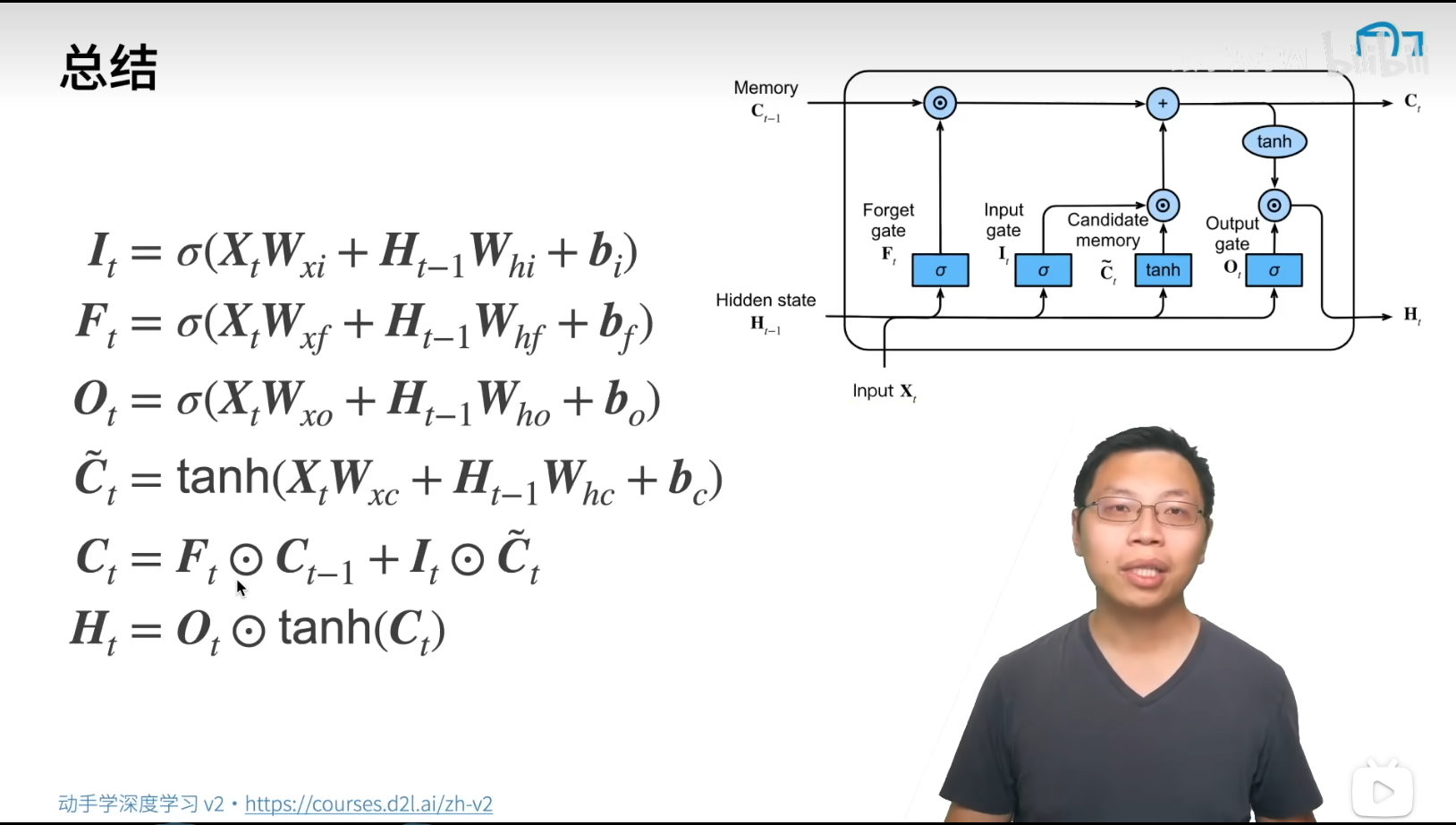
GRU&LSTM

对于一个序列, 记住相关观察需要更新门(能关注的机制) + 重置门(能遗忘的机制)

$R_t = \sigma (X_tW_{xr} + H_{t-1}W_{hr} + b_r)$ reset gate

$Z_t = \sigma (X_tW_{xz} + H_{t-1}W_{hz} + b_z)$ update gate

候选隐状态

$H_{cand(t)} = tanh(X_tW_{xh} + (R_t \odot H_{t-1})W_{hh}+b_h)$

$R_t$ : $[0,1]$ 软控制

$H_t = Z_t \odot H_{t-1} + (1 - Z_t) \odot H_{cand(t)}$

隐藏层多大? 例如 128,256, 长序列就 1024

实际不考虑 RNN, 一般 GRU/LSTM

超过 100,1000 这样的长度量级, 考虑 Attention

LSTM

忘记门: 将值朝 0 减少

输入门: 决定是不是忽略输入

输出门: 决定是不是使用隐状态

更深(多个隐藏层)的 RNN, 更多的非线性性

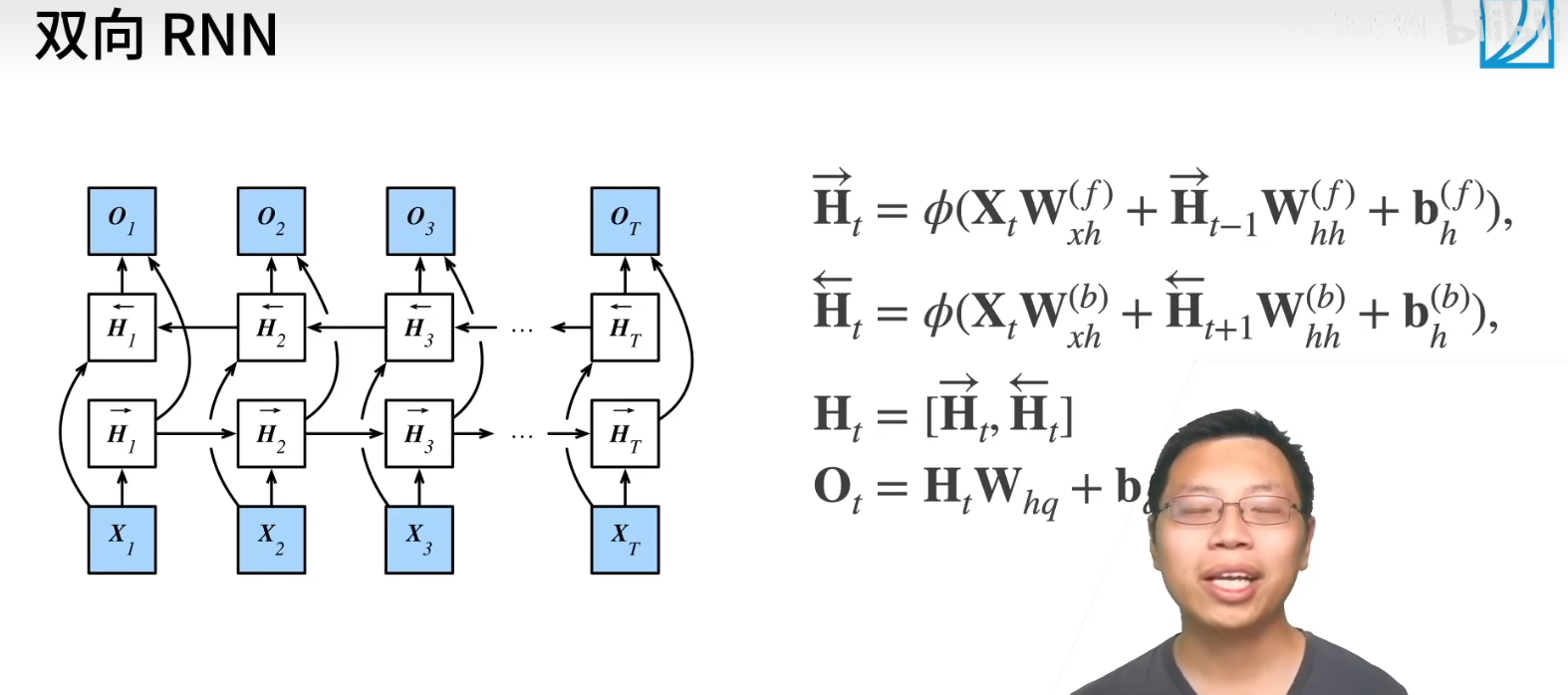
双向 RNN

一个前向 RNN 隐层

一个反向 RNN 隐层

合并两个得到输出

output 是前向和反向的共同贡献

推理怎么推? 非常不适合做推理, 几乎不能推

主要作用: 对句子做特征提取, 填空, 而不是预测未来

输入需要定长(为了以 batch 的形式读入)

如何做不定长的? 填充或者截断, 例如翻译

encoder-decoder 架构

encoder: 将输入编程成中间表达形式(特征)

decoder: 将中间表示解码成输出

encoder 将 state 传给解码器做输入

seq2seq

encoder 是一个 RNN, 可以双向

decoder 是另一个 RNN

编码器是没有输出的 RNN

encoder 最后时间步的 hidden state 作为 decoder 的初始 hidden state

训练, 训练时 decoder 用目标句子作为输入

衡量生成序列的好坏: BLEU

exp 项: 防止 pred 句子长度过短偷懒提高精度

BLEU 越大越好

seq2seq: 从一个句子生成另一个句子

sequence_mask：在序列中屏蔽不相关的项(padding)

拓展 softmax 来屏蔽不相关的预测(padding 对应的 output)

预测

最开始输入 <bos>, 然后 RNN 每次输出作为下一个的输入

seq2seq 可以纯 transformer

束搜索

beam search

seq2seq：用当前时刻预测概率最大词输出（贪心）

但贪心很可能不是最优的

暴搜指数级增长肯定不行

bin search: 对每个时刻, 保存最好的 K 个序列

每一次新预测会对 k 的 kn 个可能的下一个序列之中再调最好的 k 个

如何选择 "最好"?

单纯的概率乘总是倾向于选择短句子, 需要给长句子加权

每个候选的最终分数 $\frac{1}{L^{\alpha}}logp(y_1,...y_L)$ , 取 $\alpha=0.75 < 1$ 给长句子加权

Attention

卷积, 全连接, 池化只考虑“不随意”的线索

"最大值", 明显的特征

注意力机制显式地考虑随意线索

随意线索被称为查询 query
每个输入是一个值 value 和不随意线索 key 的对
通过注意力池化层来对有偏向性的选择某些输入

非参(不需要任何先验参数)注意力池化层

给定数据(环境, 先验, context) $(x_i,y_i)$

查询: 给定一个 x, 求对应的 $y=f(x)$

注意力: $f(x)=\sum_i \alpha(x,x_i)y_i$ , $\alpha(x,x_i)$ 就是注意力权重

最简单的方法: 平均池化, $f(x)=\frac{1}{n}\sum_i y_i$

更好的方案是 60 年代的 Nadaraya-Watson 核回归

$f(x)=\sum_{i} \frac{K(x-x_i)}{\sum_j K(x-x_j)}y_i$

高斯核 $K(u)=\frac{1}{\sqrt{2\pi}}exp(-\frac{u^2}{2})$

$f(x)= \sum_{i} softmax(-\frac{1}{2}(x-x_i)^2)y_i$

参数化:

再引入可以学习的 w

$f(x)= \sum_{i} softmax(-\frac{1}{2}((x-x_i)w)^2)y_i$

相较非参的注意力, 变得更不平滑

拓展到高维度 $\alpha(q, k_i)$

Additive Attention: 可学参数 $W_k \in R^{h\times k}$ , $W_q \in R^{h\times q}$ , $v \in R^{h}$

$a(k,q) = v^{T}tanh(W_kk + W_qq)$

等价于将 kv 合并之后放入一个隐藏大小为 h, 输出大小为 1 的单隐藏层 MLP

也是当 q, k 不一样长的时候最常用的做法

如果 q, k 都是同样长度的

2.Scaled Dot-Product Attention

$a(q,k_i)=<q,k_i>/\sqrt{d_k}$ , 相当于 q 在 k 基上的分量+归一化

$a(Q,K)=QK^{T}/\sqrt{d}$

$f=softmax(a(Q,K))V$

Q, K, V 是一个矩阵？self-attention 自注意力 $f=softmax(XX^{T}/\sqrt d))X$

但实际运用会给 X 做不同线性线性变换后再输入

$f=softmax(XW_QX^{T}W_K/\sqrt d))XW_V$

Attention 机制的 seq2seq

翻译的词可能相关于原始句子之中不同的值

原始 seq2seq 只能看到单一词的输入, 虽然有隐藏层, 但长距离丢失信息

encoder 的对每个词的输出作为 key 和 value（key = value）
decoder RNN 对上一个词的输出是 query
attention 的输出和下一个词的 embedding 合并进入 decoder

原始的 seq2seq 相当于是只将上一个词的 state+t-1 时刻的 encoder 输出丢到了 decoder 里面

$decoder(state_{t}, eoutput_{t}, output_{t-1})$

现在拓展其表达力, 认为 decoder 应该获取的不是单单最后一个词的输出, 而是和之前的词输出(更长的上下文)都有点关系, 具体关系用 attention 学习, 以编码器的 output 作为 query key, 获取这个 output 最相关的上下文, 并认为翻译的文本之中也应该有类似的上下文关系

$decoder(state_t, attention(output_{t-1}, eoutputs, eoutputs))$

tokenizer: sentencepiece

embedding: 专业词, 需要调整 tokenizer, 需要添加词 pair, 需要训练新添加的 embedding, 正常领域 frozen 不动, 加 LoRA/Adapter

自注意力

self-attention

序列长度是 n, 卷积核大小 k

	CNN	RNN	self-attention
计算复杂度	$O(knd^2)$	$O(nd^2)$	$O(n^2d)$
并行度	$O(n)$	$O(1)$	$O(n)$
最长路径	$O(n/k)$	$O(n)$	$O(1)$

自注意力适合处理长文本

代价: 计算代价 $n^2$ 增长

位置编码:

和 CNN, RNN 不同, 自注意力没有记录位置的信息, 位置编码将位置信息注入到输入里

输入 $X\in R^{n\times d}$ , 叠加位置编码 P, X+P 作为自编码输入

$p_{i,2j}=sin(\frac{i}{10000^{2j/d}}),p_{i,2j+1}=cos(\frac{i}{10000^{2j/d}})$

为什么这么设计

记 $\omega_j = 1/10000^{2j/d}$ , $p_{i+\delta} = RotateMatrix(\delta \omega_j) \times p_{i,\delta}$

所以实际上是相对位置的编码

也就是对于同一个序列 j, 位置 i 有 <i, i+k> 的关系的 pair 始终是一个相同的关系

Transformer

纯基于(self-)attention

encoder-decoder 架构

multi-head attention

对同一的 QKV, 希望抽取不同的信息

使用 h 个独特的注意力池化

attention 没有时序信息, encoder 无所谓

decoder 不应该看到不该看到的信息, 需要加入掩码

计算 $x_i$ 输出时, 假装当前序列长度为 i

基于位置的前馈网络 Positionwise FFN

将输入形状 $(b, n, d)$ 变换成 $(bn, d)$ , 输出再换回来

两层全连接, 添加非线性, 做更多的特征融合

$FFN(x)=f(xW^{T}_{1})W_2$

Add&Norm: 残差+归一化

编码器的输出 y_1, ... y_n

作为解码器之中第 i 个 transformer 块之中多头注意力的 key 和 value

预测, t+1 输出

decoder 输入前 t 个预测值作为 key, value, 第 t 个预测还作为 query

Bert

nlp 的迁移学习

使用 pretrain 的模型抽取词句的特征

不更新 pretrain 模型

问题: 1. 做 embedding 的话忽略了时序信息 2.后续模型还要自己设计, 只有 embedding 似乎没有很大用处

Bert: 能不能也通过改最后一层复用?

只有编码器的 transformer

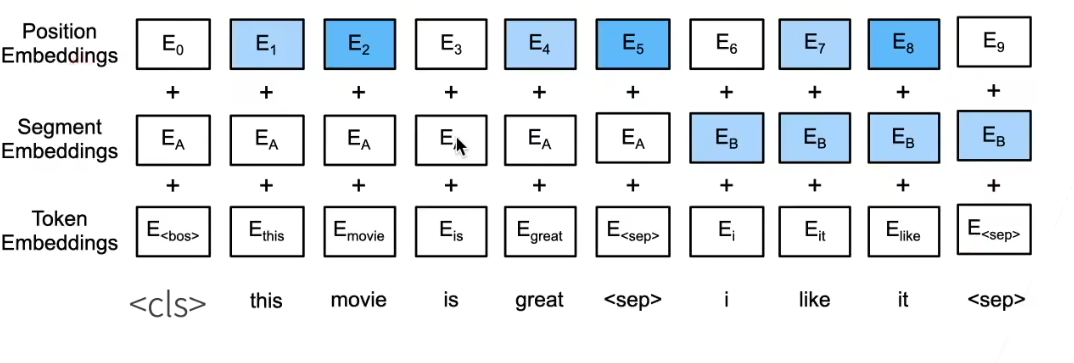
对输入的修改:

每个样本都是一个句子对
加入额外的片段嵌入
位置编码可学习

三种 embedding: position, segment, token

通用的任务?

任务 1: 带掩码的语言模型

带掩码的语言模型每次随机(15%概率)将一些词元换成 <mask>

微调任务之中不出现 <mask>

微调任务是没有 <mask> 标记的，如果设计方案是：只要 token 被选中 mask 处理，并且处理方法只要一种就是 token 别替换为 <mask>，这样的话，预训练任务和微调任务的数据太不一样了。BERT 的 3 种 mask 方法，可以使得，有 20%情况，句子对没有 <mask> 标记。

我理解的说白了就是不仅仅是因为看到了 <mask> 才去找上下文的信息，而是一直保持联系上下文的“习惯”

80%下, 变成 <mask>
10%, 随机(错误的结果)
10%, 原有(正确的结果)

10%的词会被替换成随机词元的原因：作者在论文中谈到了采取上面的 mask 策略的好处。大致是说采用上面的策略后，Transformer encoder 就不知道会让其预测哪个单词，或者说不知道哪个单词会被随机单词给替换掉，那么它就不得不保持每个输入 token 的一个上下文的表征分布(a distributional contextual representation)。也就是说如果模型学习到了要预测的单词是什么，那么就会丢失对上下文信息的学习，而如果模型训练过程中无法学习到哪个单词会被预测，那么就必须通过学习上下文的信息来判断出需要预测的单词，这样的模型才具有对句子的特征表示能力。另外，由于随机替换相对句子中所有 tokens 的发生概率只有 1.5%(即 15%的 10%)，所以并不会影响到模型的语言理解能力。（网上复制的，这是我找到的可以说服我自己的一个解释）

任务 2: 下一句子预测:

训练样本之中, 50%选择相邻句子对, 50%选择随机句子对

微调 Bert

bert 对每一个次元返回抽取了上下文信息的特征向量

不同的任务取不同的特征

句子分类, 将 <cls> 对应的向量输入到 MLP 分类
命名实体识别, 识别一个词元是不是命名实体, 例如人名机构位置
- 把每一个非特殊词元(不是 <cls><sep>...)放进 MLP 分类
问题回答: 给定一个问题和描述文字, 找一个片段作为回答
- 对片段的每一个词元预测是不是回答的开头或者结束

实用机器学习

不讲模型, 讲数据

知识积累, 学会读论文, 经典论文需要读懂每一句话

结合代码了解细节

对读过的论文做整理

前言​

下载nvidia docker runtime​

下载ollama镜像​

下载模型​

开始服务​

前端套壳​

ChatBox​

aider版本​

[可选] IDE插件​

vgg​

NiN​

GoogLeNet​

批量归一化​

ResNet​

新硬件​

多卡并行​

数据增广​

微调(迁移学习)​

目标检测​

语义分割​

转置卷积​

FCN​

样式迁移​

序列模型​

文本预处理​

RNN​

GRU&LSTM​

encoder-decoder 架构​

seq2seq​

束搜索​

Attention​

Attention 机制的 seq2seq​

自注意力​

Transformer​

Bert​

微调 Bert​

前言

下载nvidia docker runtime

下载ollama镜像

下载模型

开始服务

前端套壳

ChatBox

aider版本

[可选] IDE插件

vgg

NiN

GoogLeNet

批量归一化

ResNet

新硬件

多卡并行

数据增广

微调(迁移学习)

目标检测

语义分割

转置卷积

FCN

样式迁移

序列模型

文本预处理

RNN

GRU&LSTM

encoder-decoder 架构

seq2seq

束搜索

Attention

Attention 机制的 seq2seq

自注意力

Transformer

Bert

微调 Bert